数学问题解答

swljxdxy

小可曾于9月30日发了一个数学方面的问题，点击跟帖者不是很多。可能是问题有点离谱。小可现在解答第三个问题。（前两题已经解答了，可参阅《数学问题》中的内容。这里第三题原题为：有这样的一个结论：任何有六个人的场合，一定是其中有三个人互相认识，或者是有三个人互相不认识。“
先把6个人看成平面上的6点A、B、C、D、E和F，先看其中的5人A、B、C、D和E，若其中有3人互相认识，或者是有3人互相不认识，问题已经解决；若不满足这种情况，那就是每人都是与4人中的两人认识而与另两人不认识。为明了起见，我们这样约定：若A与B认识，则A、B用实线连起来；若A、D不认识，则A、D用虚线连起来等等。这样，可得到下图1：　　　　　　　　　　　　　　　　　　　　　　　
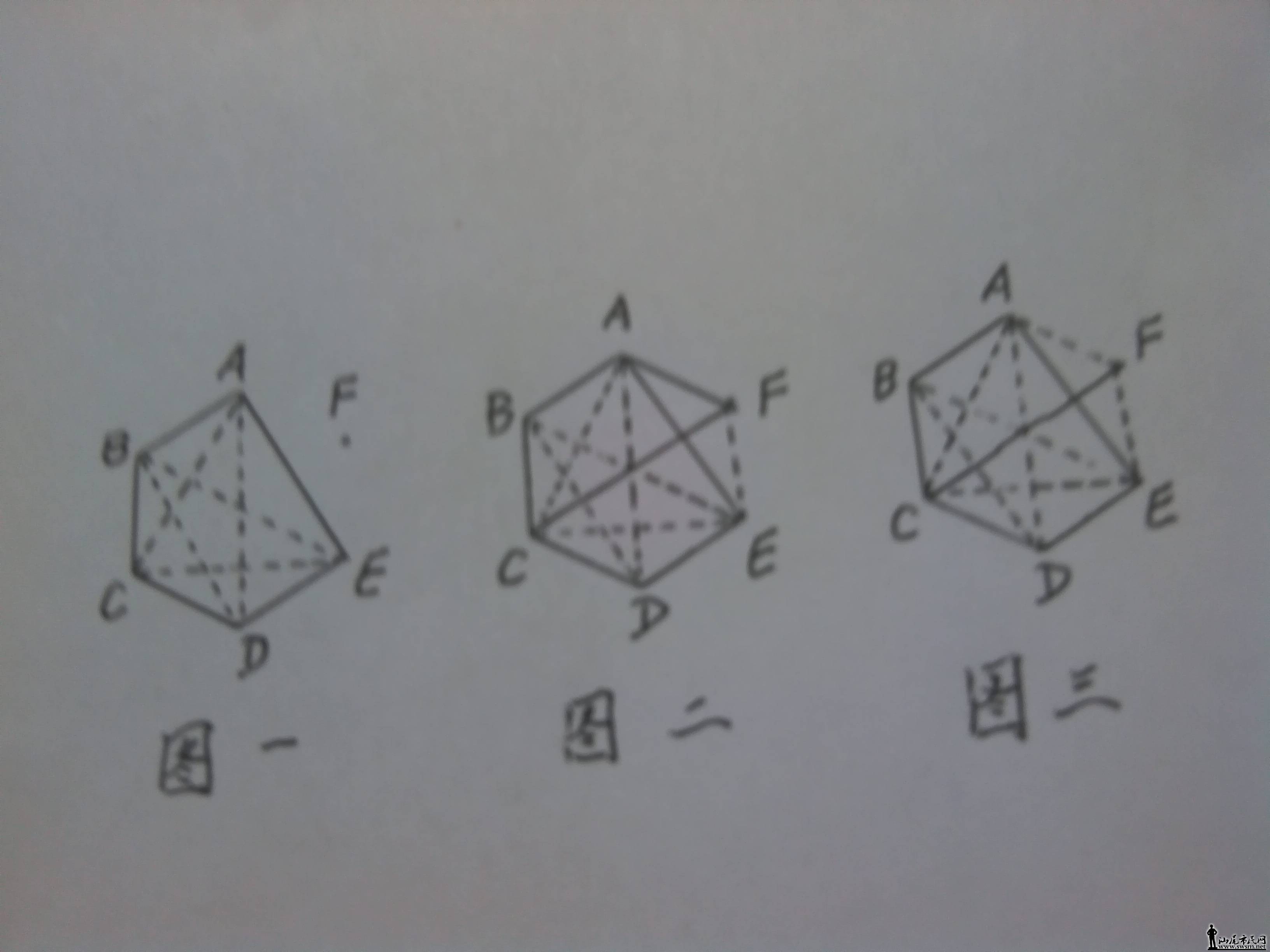
对于第六个人F，①若F与A和E都认识，则结论已明，②若F与A、E中只有1人认识，不妨设F与A认识、与E不认识，则可参阅图二（CF未连实线）。若F与C否认识，即FC为虚线，则3人F、C、E组成虚线三角形说明他们互不认识，结论成立；否则，FC为实线。这时，若FB为实线，则三角形FBC为实线三角形；若FB为虚线，则三角形FBE为虚线三角形。这说明结论也成立。③若F与A、E两人都不认识（图三，CF未连线），亲爱的网友们，你们有谁能接下去吗？（留给有心的网友）。

飞过日

9月30日发的一个数学方面的问题，怎么没看见啊？

swljxdxy

飞过日 发表于 2013-10-8 11:34
9月30日发的一个数学方面的问题，怎么没看见啊？

在《吹水》那个版块中的《数学问题》那里。可以去逛逛。

飞过日

任何有六个人的场合，一定是其中至少有三个人互相认识，或者是至少有三个人互相不认识。
这个结论是正确的。人与人，要么互相认识，要么互相不认识，可能性只有两种。从概率的角度计算，两个人互相认识（或互相不认识）的概率最大为1（100%）最小为0，平均值为50%。六个人互相认识（或互相不认识）的概率也一样。因此不论是那种情况，一定是至少有三个互相认识的或者是至少有三个人互相不认识的。

食番薯配菜补

swljxdxy

飞过日 发表于 2013-10-8 13:49
任何有六个人的场合，一定是其中至少有三个人互相认识，或者是至少有三个人互相不认识。
这个结论是正确的 ...

飞兄这样解释很好。不过这里是数学问题，必须经过严谨的数学方法才成。小可相信飞兄能够理解。

swljxdxy

食番薯配菜补 发表于 2013-10-8 13:59

谢谢顶帖！

飞过日

swljxdxy 发表于 2013-10-8 14:28
飞兄这样解释很好。不过这里是数学问题，必须经过严谨的数学方法才成。小可相信飞兄能够理解。

肥嘟嘟、

Leung-博

swljxdxy

Leung-博 发表于 2013-10-13 15:20

谢谢博兄顶帖!

Leung-博

swljxdxy 发表于 2013-10-14 10:05
谢谢博兄顶帖!

客气，我只是小年轻而已！